background and motivation
In
the
deep
ocean,
turbulent mixing of surface heat into deep
low and mid-latitude waters energetically drives the global Meridional
Overturning Circulation (MOC), which in turn controls heat transport to
higher latitudes; without deep turbulent mixing the ocean would be a
cold stagnant pool. The strength and location of the MOC depends
sensitively on the magnitude and detailed geography of ocean mixing.
Though most present generation climate models represent turbulent
mixing with a simplistic constant diffusivity, the last two decades of
ocean mixing research have instead revealed dramatic spatial and
temporal non-homogeneity in deep-ocean mixing. Climate models
that do not appropriately represent the turbulent fluxes of heat,
momentum, and CO2 across critical interfaces will not accurately
represent the ocean’s role in present or future climate. In the upper
ocean, turbulent strongly influences nutrient distributions and the
heat availble for air-sea exhange. A better understanding of the
patterns of upper ocean turbulence are necessary to correctly a variety
of things that depend on air-sea fluxes, from tropical precipitation
patterns to decadal features like ENSO.
In a global sense, the Meridional Overturning Circulation starts with sinking of dense waters at high latitudes. A large fraction of these waters return towards the surface through diapycnal, turbulent upwelling at lower latitudes, particularly in the Pacicic and Indian Oceans, as shown schematically in Figure 1.
Overall, this water mass transformation requires average diapycnal diffusivities of the order of 10^-4 m^2/s (Munk and Wunch 98, Wunsch and Ferrari 04), which is consistent with the averaged diapycnal diffusivity below the main thermocline, as measured by microstructure instruments (St. Laurent and Simmons 06, Waterhouse et al 13).
However, it has become increasingly clear that the distribution of turbulent mixing matters enormously to processes ranging from abyssal circulation to upper ocean heat storage and air-sea heat fluxes [Hasumi and Suginohara, 1999; Scott and Marotzke, 2002; Simmons et al., 2004; Gnanadesikan et al., 2004; Saenko and Merryfield, 2005; Palmer et al., 2007; Harrison and Hallberg, 2008; Friedrich et al., 2011].
Direct microstructure measurements of turbulent mixing are unfortunately spare, but techniques that allow mixing rates to be estimated using finescale parameterizations allow suggestive global patterns to emerge. For example, Whalen et al 12 use the global Argo dataset to investigate broad patterns of the turbulent dissipation rate in the upper ocean (below). They find mixing rates to vary by over two orders of magnitude, with systematic patterns that reflect the geography of processes that produce turbulent mixing. Our CPT is attempting to develop paramterizations for global circulation ocean models that not only capture this variabiity, but are based on appropriate physics that will allow the mixing rates and patters to evolve with a changing climate.
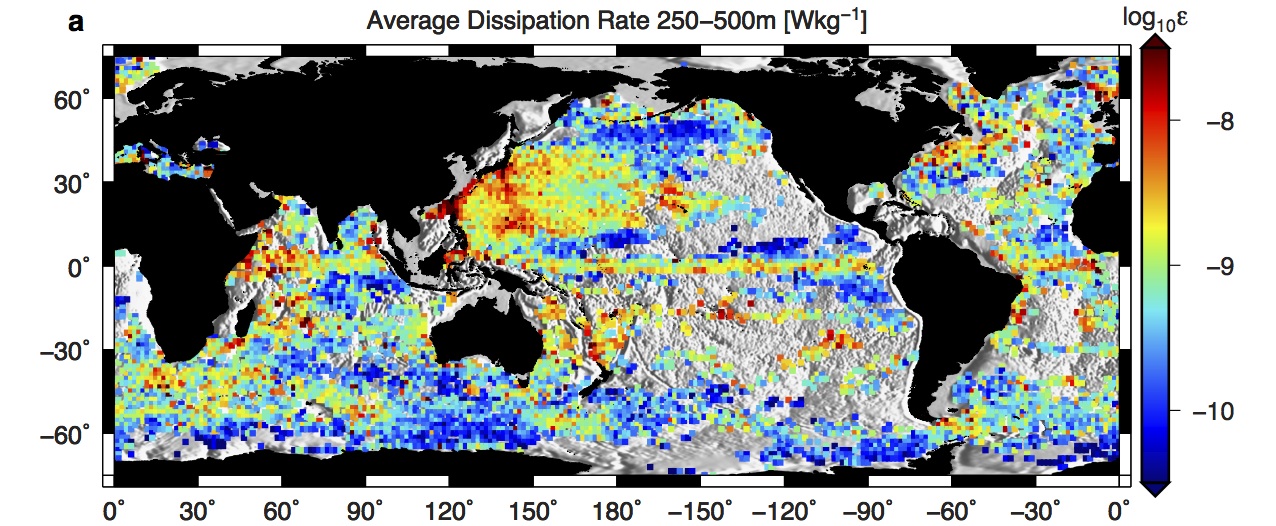
Figure 2: Diapycnal diffusivity κ (m2s−1) estimated from over five years (2006-2011) of Argo data using the finescale parameterization of vertical strain (see Whalen et al. 2012 for details). Data shown has been averaged between 250-500 m depth and over 1.5◦ square bins, and is plotted only if the bin contains more than three diffusivity estimates. The underlying bathymetry is from the Smith and Sandwell dataset (Smith and Sandwell, 1997) version 14.1.
In a global sense, the Meridional Overturning Circulation starts with sinking of dense waters at high latitudes. A large fraction of these waters return towards the surface through diapycnal, turbulent upwelling at lower latitudes, particularly in the Pacicic and Indian Oceans, as shown schematically in Figure 1.
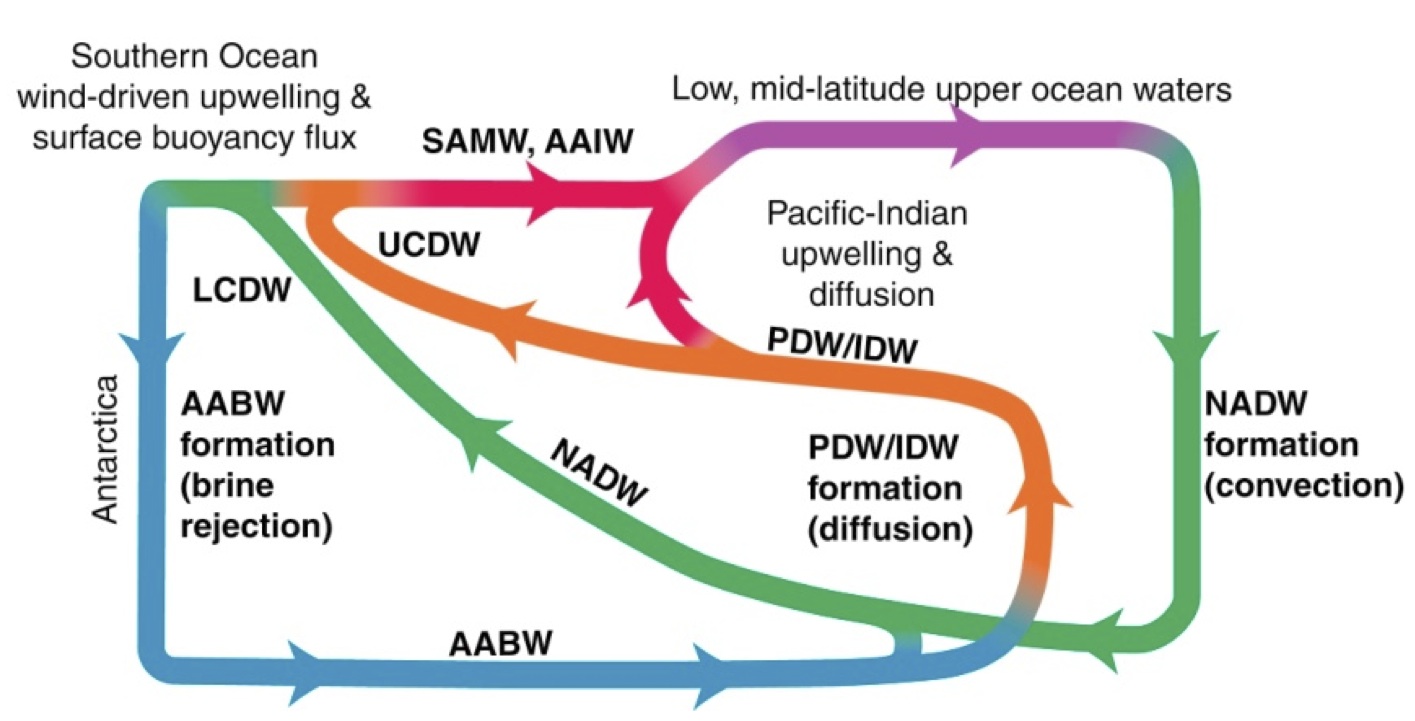 |
Figure 1: Schematic of the three-dimensional global overturning circulation, reproduced from Talley et al (2011). Here it is clear that diapycnal mixing, particularly in the Indian and Pacific Oceans, plays a fundamental role in the upwelling that ultimately returns deep and bottom waters towards the surface. |
Overall, this water mass transformation requires average diapycnal diffusivities of the order of 10^-4 m^2/s (Munk and Wunch 98, Wunsch and Ferrari 04), which is consistent with the averaged diapycnal diffusivity below the main thermocline, as measured by microstructure instruments (St. Laurent and Simmons 06, Waterhouse et al 13).
However, it has become increasingly clear that the distribution of turbulent mixing matters enormously to processes ranging from abyssal circulation to upper ocean heat storage and air-sea heat fluxes [Hasumi and Suginohara, 1999; Scott and Marotzke, 2002; Simmons et al., 2004; Gnanadesikan et al., 2004; Saenko and Merryfield, 2005; Palmer et al., 2007; Harrison and Hallberg, 2008; Friedrich et al., 2011].
Direct microstructure measurements of turbulent mixing are unfortunately spare, but techniques that allow mixing rates to be estimated using finescale parameterizations allow suggestive global patterns to emerge. For example, Whalen et al 12 use the global Argo dataset to investigate broad patterns of the turbulent dissipation rate in the upper ocean (below). They find mixing rates to vary by over two orders of magnitude, with systematic patterns that reflect the geography of processes that produce turbulent mixing. Our CPT is attempting to develop paramterizations for global circulation ocean models that not only capture this variabiity, but are based on appropriate physics that will allow the mixing rates and patters to evolve with a changing climate.

Figure 2: Diapycnal diffusivity κ (m2s−1) estimated from over five years (2006-2011) of Argo data using the finescale parameterization of vertical strain (see Whalen et al. 2012 for details). Data shown has been averaged between 250-500 m depth and over 1.5◦ square bins, and is plotted only if the bin contains more than three diffusivity estimates. The underlying bathymetry is from the Smith and Sandwell dataset (Smith and Sandwell, 1997) version 14.1.
 |
We gratefully acknowledge funding from
NSF and NOAA |
 |